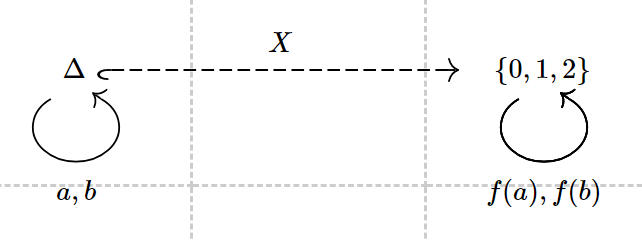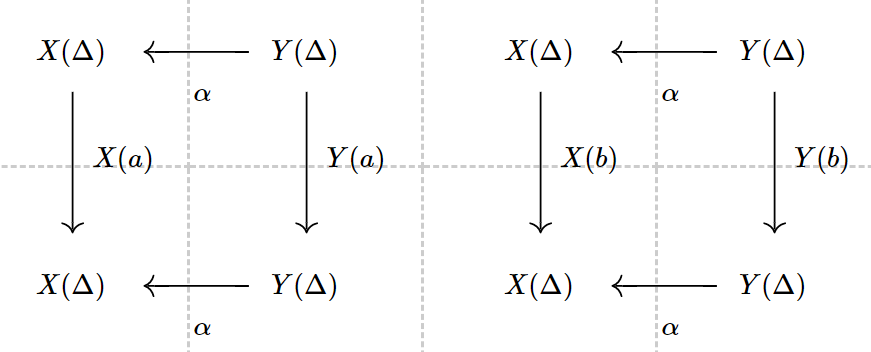The relation between DFA and Functors

当时这两颗变成紫色或绿色的灿烂星宿，想必也在闪烁吧。

Let’s consider the alphabet $\Sigma=\{a,b\}$, and $\mathcal{C},\mathcal{D}$ are two categories.

$\mathcal{C}$ is:

What really matters is:

Deterministic Finite Machine, DFA, can be regarded as the functor from monoid $(List(\Sigma),[],++)$ to the category of sets.

In fact, since $Hom_{Set}(List(\Sigma)\times S,S)\stackrel{\cong}{\rightarrow}Hom_{Set}(\Sigma\times S,S)$, so we can think the functor from $\mathcal{C}$ to Set.

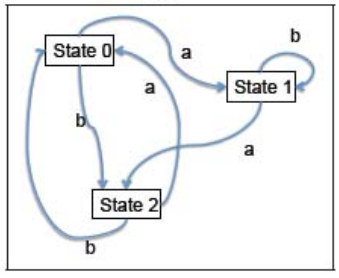
For example, consider the DFA:

it can be regarded as the functor $X$:

$$X(\Delta)=The\;set\;of\;states\;\\ X(a)=\delta_a\\ X(b)=\delta_b$$

Obviously it’s a functor from $\mathcal{C}$ to Set, although only one of the sets is involved

Then what would happen if two DFAs work equivalently?

Two DFAs accept the same language if and only if there exists a natural transformation.

---

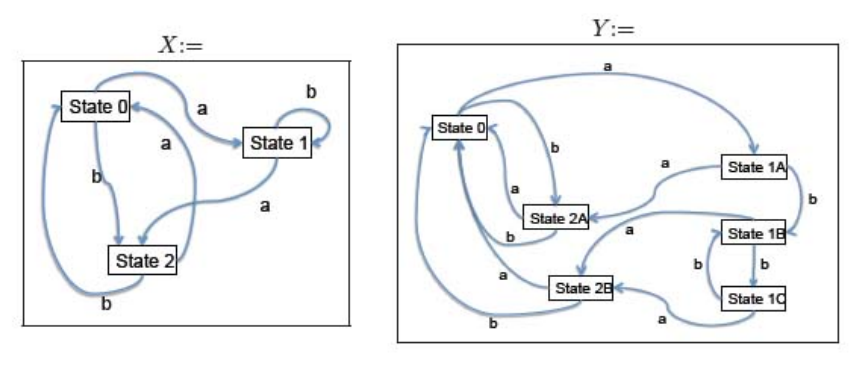
Example: consider the two DFAs as following:

They work equivalently, since we can merge state $1A,1B,1C$ and $2A,2B$ in DFA $Y$.

That means we have a natural transformation $Y\rightarrow X$.

Consider the two diagrams:

where

$$X(\Delta)=\{0,1,2\}\\ Y(\Delta)=\{0,1A,1B,1C,2A,2B\}$$

We can guarantee that there exists a function $\alpha:\{0,1A,1B,1C,2A,2B\}\rightarrow\{0,1,2\}$ making two diagrams commute.

In this example, $\alpha$ is quite obvious:

$$\alpha(0)=0\\ \alpha(1A)=\alpha(1B)=\alpha(1C)=1\\ \alpha(2A)=\alpha(2B)=2$$

Then the diagram commute:

$$\alpha\circ Y(a)(1A)=\alpha(2A)=2\\ X(a)\circ\alpha(1A)=\delta_a(1)=2$$